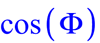Le facteur de puissance est un coefficient compris entre 0 et 1 indiquant la constance d’une charge électrique en fonction du temps. Le facteur de puissance étant le rapport entre puissance active et puissance apparente, cette dernière est définie comme la puissance absorbée si la charge était purement résistive. Un facteur de puissance égal à 1 indique une charge invariable en fonction du temps: une résistance dans son plus simple appareil présente un rapport U/I fixe. Dans le cas de tensions et courants purement sinusoïdaux, le facteur de puissance et égal au Cos(Phi), voilà c’est ici… (1). C’est l’origine du facteur puissance, dans les temps anciens les charges étaient linéaires et ne présentait que des aspects réactifs. Il faut compter à part les fours à arc électriques qui avaient déjà les propriétés de charges plus modernes comme les régulateurs de vitesse, c'est à dire des générateurs d’harmoniques et de perturbations électriques. Enfin la présence d’harmoniques dans une mesure d’intensité indique une charge variable en fonction du temps, dans ce cas le facteur de puissance est inférieur à 1 sans toutefois indiquer de déphasage entre tension et courant. 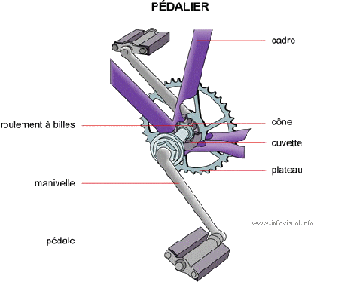Analogie: les efforts à fournir sur un pédalier de bicyclette Il transforme un mouvement linéaire, l’action des jambes sur le pédalier en un mouvement circulaire. Un facteur de puissance inférieur à un indique un pédalier dont le plateau n’est pas tout à fait circulaire, cette analogie est vraie dans le cas de charges offrant une composante réactive. L’effort à fournir varie en fonction de l’angle que font les manivelles par rapport à un plan de référence et il y a restitution de puissance pour compenser les accroissements momentanés. Un facteur de puissance inférieur à un peut indiquer des à-coups à chaque tour de pédale du fait d’un terrain gravillonné ou de jeu dans l’entrainement. Par ailleurs les vibrations transmises peuvent trouver leur correspondance dans la production d’harmoniques. On imagine bien qu’un terrain irrégulier mais considéré comme plat sur une longueur notable ne doit pas induire d’accroissement de l’énergie nécessaire au déplacement, mais les variations d’effort perçues par le cycliste vont bien générer un accroissement de la puissance nécessaire même si les efforts sont restituées dans les phases suivantes. Ceci peut expliquer la facturation supplémentaire de la part des fournisseurs d’énergie électrique lorsque les charges présentent des facteurs de puissance notables. 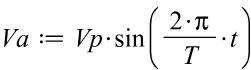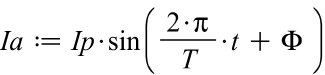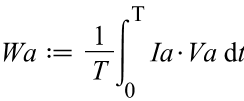(1) La valeur du coefficient de puissance en régime sinusoïdal en raison du déphasage entre le courant et la tension La tension en fonction du temps  L’intensité, déphasée de Phi par rapport à la tension  La puissance active sera égale à   La puissance apparente étant  On a donc